Image of Know your times tables, but... do you know your hash tables?

ADVERTISEMENT

Table of Contents

Introduction

Diving into the world of hash tables and understanding the underlying mechanics is extremely interesting, and very rewarding. So let's jump into it and start from the beginning.

A hash table (also known as a hash map, or dictionary) is a common data structure used in many modern day software applications. It provides a dictionary-like functionality, giving you the ability to perform operations such as inserting, removing and deleting items inside it. Let's just say I want to find what the definition of what "Apple" is, and I know the definition is stored in my defined hash table. I can query my hash table to get the definition. The entry inside my hash table might look something like this "Apple" => "A green fruit of fruity goodness". So, "Apple" is my key and "A green fruit of fruity goodness" is my associated value. Together these are referred to as a key-value pair.

One more example just so we're clear, consider the following contents of a hash table:

"bread" => "solid"
"water" => "liquid"
"soup" => "liquid"
"corn chips" => "solid"

I want to look up if "bread" is a solid or liquid, so I will query the hash table to give me the associated value, and the table will provide the answer "solid". Ok so we got the general gist of how it functions. Another important concept to note with hash tables is the fact that every key is unique. Let's say tomorrow, I feel like having a bread milkshake (which is a "liquid"), we now need to update the hash table to reflect its change from solid to liquid! So we add the entry into the dictionary, the key "bread" and the value "liquid". Can you spot what has changed in the table below?

"bread" => "liquid"
"water" => "liquid"
"soup" => "liquid"
"corn chips" => "solid"

That's right, "bread" has been updated to have the value "liquid".

Keys are unique, my bread can't be both a liquid and a solid, so each key can only appear once in a hash table.

Hash maps or arrays?

But what makes this data structure so special from the rest? Why not just use an Array instead? It depends on the nature of the problem. You may very well be better off using an array for a particular problem, and that also brings me to the point, choose the data structure that is most suited to your problem. For example, If all you need to do is store a simple grocery list, an array would do just fine. Consider the two problems below, each problem is very different in nature.

  1. I need a grocery list of fruit
  2. I need a grocery list of fruit and how much each it will cost me (per kilogram)

As you can see below, an array might be a better choice for storing the fruit for the grocery list. But a hash table looks like a better choice for looking up the cost of each item:

// Example Array
["apple, "orange", "pear", "grape"]

// Example Hash Table
{ "apple" : 3.05,
    "orange" : 5.5,
    "pear" : 8.4,
    "grape" : 12.4
}

There are literally so many opportunities to use hash tables.

Time and what that means to you

A brush up on time and space complexity.

On average it takes a Hash Table O(1) to search, insert and delete entries in the hash table. For the unaware, O(1) is spoken as "Big O 1" and represents constant time. Meaning that the running time to perform each operation is not dependent on the amount of data in the dataset. We can also promise that for searching, inserting and deleting items will take constant time, "IF AND ONLY" IF the implementation of the hash table is done right. If it's not, then it can be really slow O(n), especially if everything hashes to the same position/slot in the hash table.

Building a good hash table

So far we now understand how to use a hash table, but what if we wanted to build one? Essentially what we need to do is map a string (eg. "dog") to a hash code (a generated number), which maps to an index of an array. You might ask, why not just go straight to using indexes? Why bother? Well this way it allows us to find out immediately where "dog" is located by querying directly for "dog":

String name = Array["dog"] //name is "Lassy"

But when using an index to look up the name, we could be in the likely situation that we do not know the index where the name is located. For example, String name = Array[10] // name is now "Bob" - that's not my dog's name! And that is the benefit of mapping the string to a hash code (which corresponds to an index of an array). We can get the index of the array by using the modulo operator with the size of the hash table, index = hash_code % table_size.

Another situation that we want to avoid is having two keys mapping to the same index, this is called a hash collision and they're very likely to happen if the hash function is not properly implemented. But the truth is that every hash function with more inputs than outputs there is some chance of collision. To demonstrate a simple collision take the following two function outputs below:

int cat_idx = hashCode("cat") % table_size;    // cat_idx is now equal to 1

int dog_idx = hashCode("dog") % table_size;    // dog_idx is now also equal 1

We can see that both Array indexes are now 1! And as such the values will overwrite each other because they are being written to the same index. Like if we tried to look up the value for "cat" it would then return "Lassy". Not what we wanted after all. There are various methods of resolving hash collisions, the more popular one is called chaining. The idea with chaining is that there is a Linked List for each index of an array. If a collision occurs, the value will be stored inside that linked list. Thus in the previous example, we would get the value we requested, but it we would need to search a linked list attached to the index 1 of the array. Hashing with chaining achieves O(1 + a) time where a is the load factor which can be represented as n/k, n being the number of entries in the hash table and k being the number of slots available in the hash table. But remember this only holds true if the keys that you give are particularly random (relying on SUHA).

This is a big assumption to make, as there is always a possibility that non-equal keys will hash to the same slot. One solution to this is to take the reliance of randomness away from what keys are given to the hash table, and put the randomness on how the keys will be hashed to increase the likeliness of very few conflicts occurring. And this is known as...

Universal hashing

The concept is pretty simple, select at random a hash function h from the set universal hash family to compute the hash code. So in other words, choose any random hash function to hash the key! And by following this method it provides a very low probability that the hashes of two distinct keys will be the same. I will keep this one short, but if you don't trust me then trust Mathematics instead. Also another thing to watch out for is when implementing this method be careful of having a bad universal hash family. It can blow out the time and space complexity to O(U) where U is the size of the family. And where the challenge lies is finding a Hash family that does not take too much time to compute, and too much space to store.

A hash function of the gods

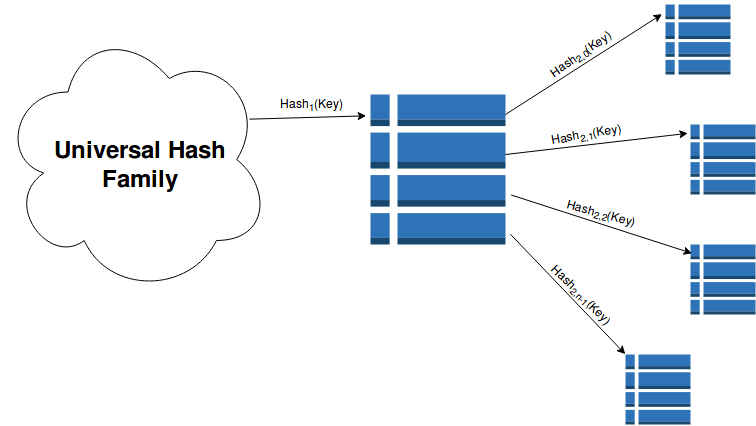
The search for perfection is inevitable. What if we could construct a perfect hash function where we could just map things to a set of integers with absolutely no collisions. Good news is we can do this, Well kind of.. but our data has to be static (which means no insertions/deletes/updates can assured constant time). One approach to achieve a perfect hash function is to use 2-Level Hashing, it is basically a combination of the last two ideas we previously discussed. It uses universal hashing to select which hash function to use, and then combines it with chaining, but this time instead of using a linked list data structure we use another hash table! Let's see how this looks visually below:

Learn hash table

But how does this work and how can we ensure no lookup collisions?

Well it works in reverse to the Birthday paradox. It states that in a set of N randomly chosen people, some pair will have the same birthday. But if the number of days in a year far outweighs the number of people (squared) then there is a damn good possibility that no pair of people will share the same birthday. So how it relates is, for each chained hash table is the size of the first-level hash table squared. That is if two elements happen to hash to the same slot, then the size of the chained hash table will be of size 4. Most of the time the chained tables will be very sparse/empty.

Repeat the following two steps to ensure no look up collisions,

  1. Select a hash from the universal hash family
  2. If we get a collision, then select another hash from the universal hash family.

Literally that is it, (Well.. for an O(N^2) space solution anyway). If space is a concern, then a different approach is obviously needed. But the great thing is that we will only ever have to do this process on average twice.

Conclusion

A hash table is only as good as it's hash function. Deriving a perfect hash function is much harder to achieve without losing in particular areas such as functionality, time, and space. I invite you to always consider hash tables when solving a problem as they offer great performance benefits and they can make a noticeable difference in the usability of your application. Hash tables and perfect hash functions are often used in real-time programming applications. And have been widely implemented in algorithms around the world. Hash tables are here to stay.

Final Notes