Image of Plain old graphs that solve your problems

ADVERTISEMENT

Table of Contents

Introduction

The graphs in computer software are a little different from the bar graphs in high school. Sure, they are still a mapping of relations just represented differently. Graphs can actually help solve a really large number of problems. They can be used to solve problems in social networking, eg. finding relations between friends or friends of friends or in GPS navigation, finding an optimal route from your house to the nearest shopping centre. Graphs are used regularly in robotics and AI, for example, sometimes for maintaining all the possible states a robot is allowed to be in (so they don't break stuff or move through walls). They're great for scheduling problems, like when to schedule traffic flow (which can be solved with graph colouring). Ahhh the list goes on, they solve so many real-world problems.

Graph representations

It's real important to understand the basic concepts of a graph, even if it might be boring, it pays you back ten-fold in the long run. So I'll start from the top..

What is a graph? Well it has those little points on it, right? Oh yeah.. and you connect those points together somehow.....voila you have a graph!

What are those points? They are called vertices or nodes. I will be using the nodes terminology for consistency.

What are the lines called? They are called edges.

Ok cool, so we get what a graph is... just nodes and edges connected in some way! Maybe looking something like this:

Nodes and edges

Some other properties that help define a graph:

  • directed - the edges only point one-way, so an example of a directed graph might be a road map only consisting of one-way streets that can you travel down.
  • undirected - the edges point both ways, you can go up and down the road.
  • weighted - weighted graphs have some sort of cost travelling down a particular edge. Eg. 30 mins to travel down street Y.
  • unweighted - no costnassociated with the edges.
  • acyclic - you will never encounter the same node twice.
  • connected - all nodes in the graph are in some way connected. If the graph was a physical model you could just pick it up and since its a connected graph it won't fall apart.
  • disconnected - the graph is made up of sub-graphs or it is bipartite.

How do we represent this in code? My answer - Many ways. It really depends on the problem as to how you should represent your graph. Here are my two go-to's...

Adjacency matrix

An adjacency matrix is used to represent a finite graph. It is important to note that if your problem is dealing with continuous space, then there are better choices to represent your graph. So what is an adjacency matrix? It is essentially just a matrix with 1's and 0's. It can be sparse (mostly filled with 0's) and each row and associated column is a node of the graph. It might look something like this:

Adjacency matrix

So now we have a relationship that is a directed edge looking something like 0 -> 9. If we want an undirected relationship then we must look up row 9 and column 0 then write a 1 to the matrix to denote that there is an edge between 9 and 0. Now an undirected edge will look something like this 0 <-> 9, making it bidirectional (functions in both directions).

But why use an adjacency matrix? That f****** godly lookup speed. It's possible to directly query the graph to see if it has a connection between two nodes by simply looking up the index of the matrix, eg. matrix[i][j] where i is the row, and j column. This performs at O(1) constant time because you don't waste time searching through the entire matrix for what you need.

It can't be all good? It's not. If you're space conscious, adjacency matrices take up lots of space. To be precise O(V2), where V is the number of nodes in the graph. This is simply because it stores every possible combination of edges between nodes. Even if they are '0's (denoting no edge between 2 nodes). It also takes extra time to look up adjacent nodes it has to search through all nodes in the graph. Not very efficient.

I would pick an adjacency matrix if the amount of nodes in your graph is relatively small and you need the fast access times.

Adjacency List

These are my favorite. Adjacency lists are used to represent a finite graph. They are essentially just a list of all nodes. But each node in the list maintains a pointer to a list of all its neighbouring nodes. Something like this:

Adjacency list

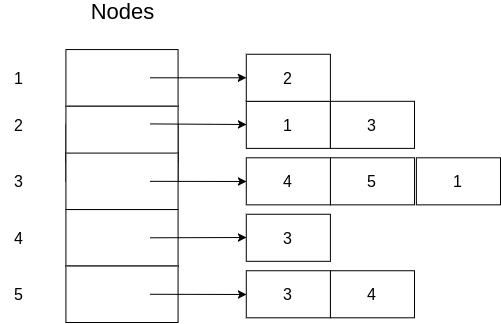
This can be easily implemented using a hashtable! If you haven't read my post on hash tables, check it out for details on how they work under the hood. Now... how can we implement this using a hashtable? Simple. One approach could be by using an object-oriented approach and representing the nodes of your graph as objects. Then inserting each Node object into your Hashtable as a key and the list of neighbouring Node objects as the value. (The list of neighbours can be empty).

So ok.. why are these good? Adjacency lists are a good graph representation because it's possible to retrieve all the neighbours of a node in constant time O(1). How could we translate this to a real-world problem? Hmm...

Maybe finding out all friends of some person 'X' in a social network. Thinking about this problem... a Node object could be replaced with a Person object and properties of the Person object could be name, dob, age etc. then we can just do a lookup of the hashtable for person 'X', then receive back a list of all the Person objects a.k.a all friends in their social circle.

We've been through a brief intro on how to actually represent a graph. Now, what if we wanted to use that graph? The time has come my friend. We can search for our answers.

This topic is extremely broad and there are so many search methods. I will go through the popular ones, hopefully also touching on some more advanced search methods. One thing to note is that we will always want to end up in some goal state, so by finding a "goal node". But to do that, we must start at some "initial node" and travel through some path to reach the goal. In graph world, the "initial" node can also be referred to as the "root" node. I will use "root" and "initial" interchangeably.

DFS or Depth-first search is a method used for searching a graph. It starts off the search at the root node, selects a neighbouring node, then it starts exploring until all connected nodes have been explored. You can think of it as going down a tree, exploring all child nodes until it hits the bottom of the tree. Then it comes back up, and selects the next neighbouring node and repeats the process expanding down the tree. But what if I had millions of nodes in my graph and I was looking for my goal node? Hmm that could be a problem, especially if the branching factor is quite large. But if the goal node is very deep in the tree it could also work quite well. It is very hard to say as usually depends on the problem.

Implementing a DFS? Use a Stack! The pseudocode for DFS is as follows:

DFS(Graph, root, goal):

   let S be a stack
   S.push(root)
   while S is not empty
       node = S.pop()
       if node is the goal:
          return node
       if node is not labeled as discovered:
           label node as discovered
           for all edges from node to neighbour in Graph.adjacentEdges(node) do
               S.push(neighbour)

BFS or breadth-first search is another method for searching a graph. This is most-of-the-time preferred over using DFS, as it explores the graph by "levels". It has a more even search in nature. If the goal node somewhat closer to the root node, then BFS is probably a better choice than DFS. How does BFS do its thing? It starts its search from the root node, expands all the neighbours in the first level (those which are directly connected to the root). Then it selects a neighbour, and expands all the nodes in its first level. After that, it goes back and selects the next connected node/neighbour and expands all of its nodes in its first level. The process is repeated until the goal node is finally found.

Implementing a BFS? Use a queue! The pseudocode for BFS is as follows:

BFS(Graph, root, goal):

   create empty set S
   create empty queue Q

   root.parent = null
   add root to S
   Q.enqueue(root)

   while Q is not empty:
       current = Q.dequeue()
       if current is the goal:
           return current
       for each node n that is neighbour of current:
           if n is not in S:
               add n to S
               n.parent = current
               Q.enqueue(n)

Both DFS and BFS are classified as an "uninformed" search method as they're blindly searching for the goal node. Another thing to add is that it is extremely helpful to understand how these algorithms work through visual representation. This way you can see how the algorithm is suppose to work, making it easier to represent in code. Check out these two links below:

Youtube clip demonstrating DFS Youtube clip demonstrating BFS

Ok now question is... can we do better than BFS or DFS? What if there was a way to "inform" our search and to only expand the nodes in the optimal path to the goal node..

The A* search is an extension of dijkstra's algorithm, which is used to get the shortest path between two nodes. What makes A* different? It uses a heuristic to guide its search in the direction of the goal node. For our A* search to work as expected, then we must have a heuristic which is admissible. This means it should never overestimate the cost of reaching the goal node, shown as the following - h(n) <= h*(n), where h*(n) is the cost to reach the goal from n.

It applies a cost function to each neighbouring node from the current node. If we were beginning the A* search, the current node would be the initial starting node. It would then apply the cost function to each of its neighbouring nodes. The cost function in A* is represented as f(n) = g(n) + h(n), where f(n) is the total estimated cost to reach the goal node, g(n) is the estimated cost to get to the node and h(n) is our heuristic for estimating the cost to reach the goal node from n.

Implementing an A* search? Use a Priority Queue! The pseudocode for A* is as follows:

A*(Graph, root, goal):

  initial = root
  create empty PriorityQueue Q

  Q.add(initial)
  While Q is not empty:
     current = Q.remove()
     label current as visited
     if current is the goal:
        return current
     for each node n that is neighbour of current:
        g(n) = g(current) + cost(n)
        f(n) = g(n) + h(n)
        Q.add(n, f(n))
        set node to be child of current

When we call remove() from the Priority Queue, we are assuming that it removes the node with the minimum f value which was calculated using the cost function f(n). You might be wondering where does this heuristic come in? Remember.. it was used to calculate f(n). One thing to note is that if h(n) = 0, then f(n) will just be g(n) which is just the estimated cost to get to the node. The algorithm then reverts back to dijkstra's algorithm, guaranteeing a shortest path. If h(n) is the exact cost to get to the goal node, then the A* will never expand nodes not in the optimal path to the goal node. Making the algorithm blazingly fast.

So in order for A* to be optimal, its heuristic h(n) must never overestimate the cost of reaching the goal node AND... be consistent.

What is a consistent heuristic? A heuristic is consistent if the cost from your current node to a neighbouring node plus the h value of the neighbouring node is less than or equal to the h value of the current node. cost(current, neighbour) + h(neighbour) <= h(n) WTF does that mean? The solution will always give the shortest path no matter what node you start at.

What happens if the heuristic fails? (It overestimates the cost of the goal). Well... then your algorithm will misjudge the nodes that are actually worthwhile expanding. And not perform optimally.

We can use A* for also searching in continuous space, where essentially there is a never ending amount of graph. It's possible to discretize the graph and use A* to search through the discretized version to find your goal node (or state).

Conclusion

Graphs can be constructed in so many ways and used to solve many problems. When considering to use a graph, a good practice is to model your problem and try to adapt it to a graph scenario. Does it fit well? If yes, then awesome! use a graph. There is plenty of technology available to build your solution and just about every programming language has the data structures available in their standard libraries. There is always more to learn with graphs and I hope this post has sparked your interest of graphs as it did mine!

Final Notes